Optimizing Strategies for Selection on Major Genes
Department of Animal Science
Iowa State University
225 Kildee Hall
Ames, IA, 50011
Introduction
To date, most genetic progress for quantitative traits in livestock has been made by selection on phenotype or on estimates of breeding values derived from phenotype, without any knowledge of the number of genes that affect the trait or the effects of each gene. In this quantitative genetic approach to genetic improvement, the genetic architecture of traits of interest has essentially been treated as a ‘black box’. Despite this, the substantial rates of genetic improvement that have been achieved and continue to be achieved for the main livestock species based on this quantitative genetic approach, are clear evidence of the power of this method of selection.
The success of quantitative genetic approaches to genetic improvement does, however, not mean that we could not make more progress if we could gain insight into the genetic black of quantitative traits and used that information to make better selection decisions. By being able to study the genetic make-up of individuals at the DNA level, molecular genetics has given us the tools to make those opportunities a reality. To date, molecular genetic techniques have already resulted in the discovery of several genes that have a major effect on some quantitative traits of interest (so-called quantitative trait loci or QTL) and of genetic markers that are linked to QTL. As an example of progress that has been made in this area, Rothschild (1998) recently documented evidence of over a dozen major genes and marked QTL that have been identified for economic traits in swine. Prime examples are the ryanodine receptor gene (halothane gene) for meat quality, the estrogen receptor gene for litter size, and genetic markers for QTL for growth, backfat, litter size and disease on several chromosomes. Despite these advances, it must be pointed out, however, that the QTL that have been identified to date only represent the tip of the iceberg and that the majority of genes for the traits of interest have not (yet?) been detected. These genes, therefore, continue to reside in the ‘black box’ domain. This leads us to the situation that is depicted in Figure 1, in which we have detailed information on some genes but must continue to rely on phenotypic data for the majority of genes. This situation will remain reality for the foreseeable future, until all genes have been sequenced and identified.
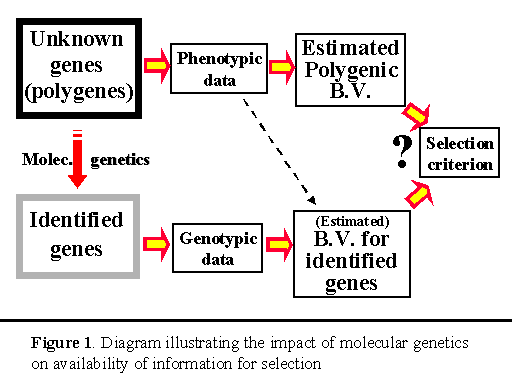
Once a major gene or QTL has been discovered, an
important practical question remains on how
to use this gene to enhance rates of genetic progress. This is the main
topic of this paper, in which I will limit myself to the use of a
known major gene to enhance selection for a quantitative trait in
an outbred population or line. For simplicity, we’ll consider a single
major gene with two alleles (B and b) with frequencies p and q and with
known genotypic values that are equal to –a (bb), d (Bb, and +a (BB).
Following Falconer and Mackay (1996), breeding values for this major
gene are then equal to +2qa, (q-p)a, and -2pa,
respectively, for the major genotypes BB, Bb, and bb, where a=a+(q-p)d is the average allele substitution
effect. Or, when deviated from the heterozygote, breeding values are
equal to a, 0, and
-a (see Figure 2). We’ll also assume that all
individuals are genotyped for the major gene prior to the age of
selection. It what follows, I will refer to all the other unknown genes
that affect the trait as polygenes and to their collective effect
on the trait as the polygenic effect or polygenic breeding
value.

One of the approaches to use this major gene in a selection program would be to fix the B allele as quickly as possible by selecting only individuals that have one or preferably two copies of the B allele (i.e. Bb and BB individuals). Although this approach would lead to fixation of the gene within a couple of generations, depending on gene frequency and selection intensity, this strategy would not result in greatest response to selection for the trait. This is because the major gene is only one of the genes that affects the trait, albeit a major one, and no selection pressure is applied to the polygenes in this selection process. The shortcomings of this approach were clearly demonstrated by Muir and Stick (1998), who showed that selection strategies that aim to fix the major gene as quickly as possible achieve less response to selection than traditional selection based on phenotype, both in the short and the longer term.
The main lesson from the work of Muir and Stick (1998) is that, if we want to improve the phenotypic performance of a population, we must focus on the total genetic value of the trait and not just on the one or few genes that we happen to know something more about. Although the major genotype provides (accurate) information on the animal’s genetic value for one of the genes that affect the trait, an individual’s phenotypic performance can be used to estimate the animal's genetic value for all the other ‘black box’ genes (the polygenes), like we have always used phenotypic data. Although the resulting estimate of the polygenic breeding value may not be as accurate as the estimate for the major gene, maximum genetic progress will be made by using both estimates, rather than basing selection on only one of them. The question then becomes how we can best combine these the estimated breeding value (EBV) for the major gene with the EBV for the polygenes (see Figure 1).
One way to combine the molecular genetic and phenotypic information is to select on the simple sum of the two estimates of breeding values and select on the following criterion:
I = Major Gene (E)BV + Polygenic EBV
In theory, this simple sum of the best estimates of breeding values for the major gene and polygenes gives the best estimate of the animal’s total breeding value. If both estimates are based on BLUP from an animal model, their sum gives the BLUP of the individual’s total breeding value. In theory, selection on this criterion should maximize response to selection from the current to the next generation. The question, however, is whether selection on this criterion for several generations would also maximize response in the longer term.
Gibson (1994) used stochastic simulation to compare selection on the above selection criterion (I), which will be referred to as genotypic selection in what follows, to phenotypic selection, in which the information from the major gene was not used. He found that, although genotypic selection resulted in greater cumulative response to selection in the short term, phenotypic selection achieved greater response in the longer term. This is illustrated in Figure 3. This figure also shows that, although genotypic selection fixes the major gene more rapidly, this is at a cost of response in polygenes. With genotypic selection, the polygenic response that is lost in the initial generations, as the major gene is selected toward fixation, is never entirely recovered in later generations.
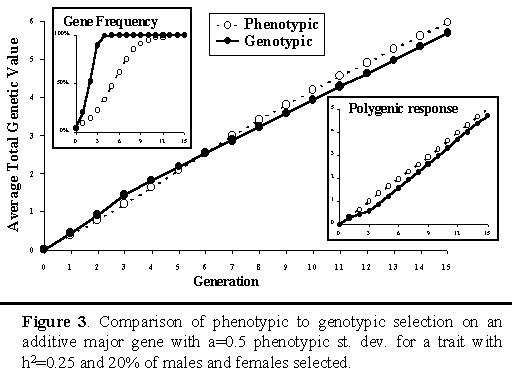
The results of Gibson (1994) have been confirmed in several other studies that simulated selection on a known major gene (e.g., Woolliams and Pong-Wong 1994), including studies in which polygenes were simulated based on a finite number of loci instead of based on the infinitesimal genetic model of quantitative genetics (Kuhn et al 1997, Fournet et al. 1997). All these studies, however, assumed the effect of the gene was known, compared selection on the major gene to selection on the animal’s own phenotype only, and assumed phenotype was observed on all animals. Other studies have removed one or more of these limitations by considering selection on linked genetic markers or marker brackets, selection on Best Linear Unbiased Predictors of breeding values from an animal model, or selection for a trait that is not measurable in both sexes or on live animals (e.g. Van der Beek et al. 1994, Ruane and Colleau 1995 and 1996, Meuwissen and Goddard 1996, Larzul et al. 1997). These studies did not consistently find that longer-term responses were less with use of marker information (marker-assisted selection) than responses from traditional selection. All studies did, however, find that the advantage of marker-assisted selection over traditional selection declined in later generations. These studies also did not establish that the applied strategies for marker-assisted selection maximized responses to selection in the longer term, as well as in the short term. Given the suboptimality of genotypic selection on a known major gene, as found by Gibson (1994) and others, it seems clear there may be scope to further improve responses from marker-assisted selection in these situations also.
The literature described above has cast important questions on how identified genes should be used in selection. Although the main implication from this work is that selection on the genotypic selection criterion shown above may not maximize response in the longer-term, it also raises the question whether the genotypic selection criterion makes optimal use of the major gene in the short-term. Therefore, the issue raised by Gibson (1994) is important not only one for the longer-term but also may have important implications for the shorter term. The objectives of the research that will be presented in what follows were to resolve these issues. Specifically, our objectives were:
- to develop methods to optimize selection on an identified major gene.
- to compare the benefits of optimal over genotypic and phenotypic selection.
Methods to address these objectives were developed based on a simplified breeding program and genetic model. Although extensions to more complicated and realistic models are needed prior to application, this simplified model allowed development of a framework for optimization of more complex situations and serves to illustrate issues and concepts.
Methods
A deterministic model for selection in a population of infinite size with discrete generations was developed. Selection was for a quantitative trait that was affected by a major gene and polygenes. Polygenic heritability was h2 and assumed unaffected by selection. The major gene had two alleles (B and b), with genotypic values –a, d, and +a for the three genotypes (see Figure 2).
In general, selection was by truncation selection on an index that combined the breeding value for the major genotype (a, 0, and -a for BB, Bb, and bb) with an estimate of the polygenic breeding value:
Iopt = b*(Major Gene BV) + Polygenic EBV
Polygenic EBV were estimated based on the individual’s phenotype as h2(phenotype – major genotype value). Different weights on the major gene were allowed for, depending on the animals major genotype, sex, and generation. Note that with genotypic selection all weights are equal to 1. For optimal selection, the objective was to find the index weights that maximized cumulative response after T generations. This objective can be formulated as:
GT = (psT +pdT -1) a + (psT +pdT -2 psT pdT ) d + AT
where psT and pdT are the frequency of the B allele among selected sires and dams, respectively, that produce generation T, and AT is the average polygenic breeding value in generation T.
Optimal index weights were derived by formulating this multiple stage decision problem as an optimal control problem (Lewis, 1986; Dekkers et al. 1995). Iterative procedures for finding the optimum were developed based on optimal control theory (see Dekkers and van Arendonk 1998 for details).
Results
Figure 4 shows cumulative responses for phenotypic and optimal selection relative to cumulative response achieved with genotypic selection on an additive major gene. For each generation, cumulative responses to phenotypic and optimal selection are shown as a percentage of cumulative response to genotypic selection. For optimal selection, three different strategies are shown, depending on whether the objective was to maximize cumulative response at the end of 3, 5, or 10 generations.
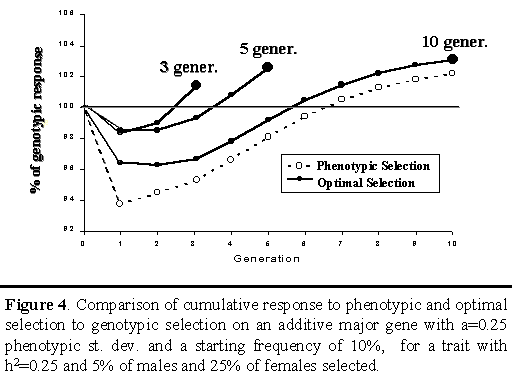
Results for phenotypic selection are similar to those in Figure 1, showing less response from phenotypic selection in the initial generations but greater response in later generations (Figure 4). For optimal strategies, only the cumulative response in the last generation is of relevance, since the objective here was to maximize response at the end of the planning horizon (3, 5, or 10 generations). Results indicate that optimal selection did indeed receive greater cumulative response at the end of its planning horizon than either genotypic or phenotypic selection. Although the differences were not large (up to 3% extra genetic improvement over genotypic selection at the end of the planning horizon), the results demonstrate that greater response to selection can be obtained from optimal use of a major gene, in the short as well as the long term.
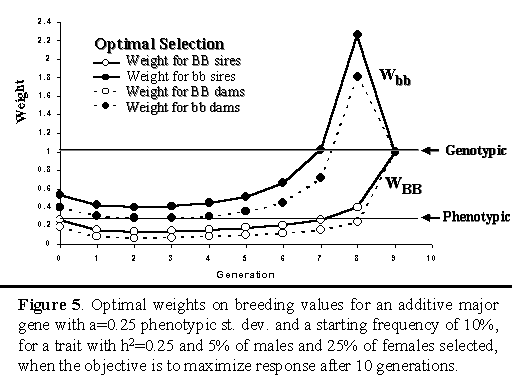
Figure 5 shows the optimal weights on the breeding
value for the major gene for the strategy that maximized cumulative
response after 10 generations.
Note that genotypic selection applies a constant weight of one across
generations. Phenotypic selection implicitly applies a weight equal to
heritability to the major gene. For optimal selection, weights changed
from generation to generation, as frequency of the major gene changed
and the population moved closer to the end of the planning horizon.
Except for the last three generations, optimal weights were close to the
implicit weight for phenotypic selection (h2). In any
generation, weights were higher for selection of males than females,
wich is related to the greater selection intensity among males. Weights
on the breeding value for the major gene were also greater when the
individual was bb versus BB. In essence, this implies that the optimal
selection strategy increased the frequency of the favorable major gene
allele to a greater degree by selection against bb genotypes than
by selection in favor of BB.
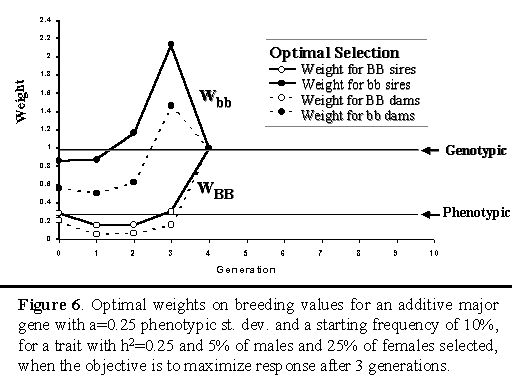
Figure 6 shows the optimal weights when the objective was to maximize cumulative response after three generations for an additive major gene. For this objective, the optimal strategy put greater emphasis on the major gene than when the objective was to maximize response over 3 generations.
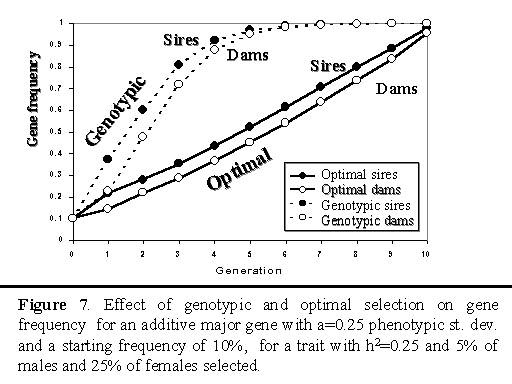
Figure 7 illustrates how frequency of the B allele changed with genotypic and optimal selection on an additive major gene over 10 generations. With genotypic selection, the major gene was moved to fixation within 6 generation. Optimal selection showed a gradual and almost linear increase in frequency, with fixation at the end of the planning horizon.
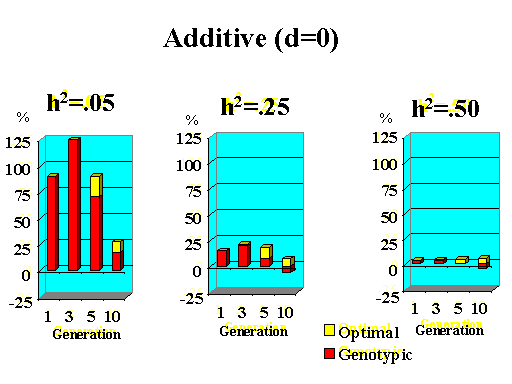
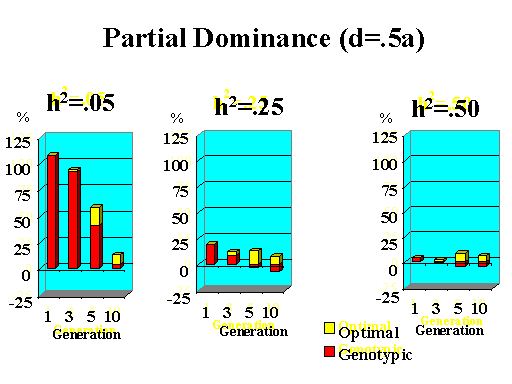
Previous results applied to a major gene with additive effects. Figure 9 shows the extra response that can be expected from selection on the major gene through genotypic and optimal selection for a major gene with various degrees of dominance. Results show how much extra response over phenotypic selection can be expected from genotypic and optimal selection for four planning horizons (1, 3, 5, and 10 generations) and three levels of (polygenic) heritability (5, 25, and 50%).
| Figure 9. Extra response from genotypic and optimal selection over phenotypic selection (% extra response) for a major gene with different degrees of dominance for a trait with different polygenic heritabilities. The major gene has an additive effect (a) equal to 1 genetic standard deviation for polygenes and a starting frequency of 10%. Fractions selected among males and females are 25 and 50%. |
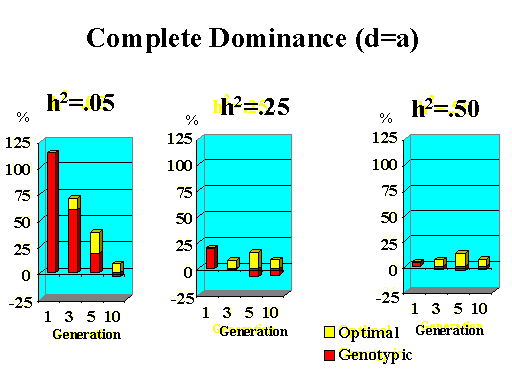
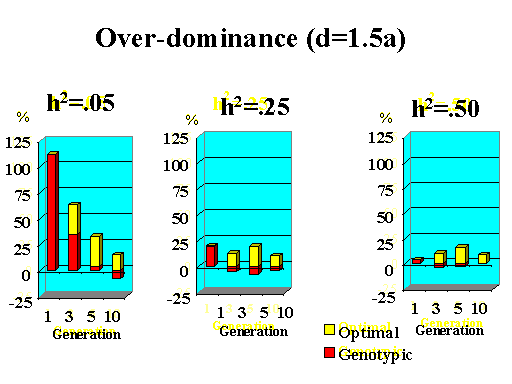
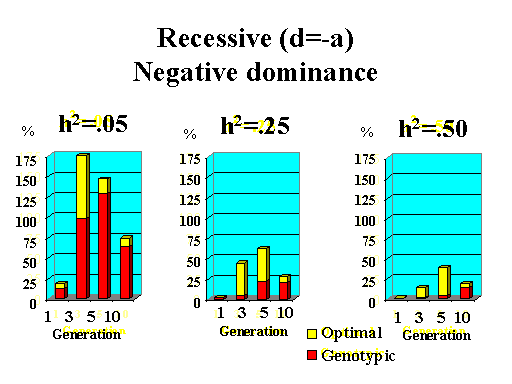
|
Extra response from selection on the major gene through genotypic selection was greatest for traits with low heritability and for short planning horizons (Figure 9). Genotypic selection resulted in similar or less response than phenotypic selection for longer planning horizons and higher heritabilities. Degree of dominance at the major gene did not have a large impact on the extra response that can be expected from selection on the major gene through genotypic selection for the parameters studied here, except when the major gene had negative dominance (recessive). For such a gene, extra response was greater for intermediate to longer planning horizons. It must be pointed out, however, that these results vary depending on the specific parameters used (i.e. size of the major gene effect, starting frequency at the major gene, and fractions selected).
The extra benefit that can be expected from optimizing selection on the major gene over selection on the major gene through genotypic selection is also shown in Figure 9. Greater benefits from optimal selection were found as dominance at the major gene increased. For major genes with complete or over-dominance, optimizing selection on the major gene resulted in substantial extra responses of up to 25% for longer as well as short planning horizons. For a recessive major gene, extra responses of up to 75% were found for a planning horizon of only three generations for a trait with low heritability. Again, these results depended greatly on parameters such as size of the major gene, starting frequency, and fractions selected, so the results shown here serve as illustration for the potential benefits that can be expected from optimizing selection on a major gene.
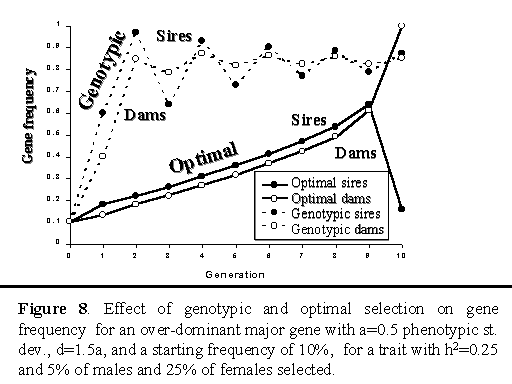
Figure 8 shows trends in gene frequencies for genotypic and optimal selection on a major gene with over-dominance. For genotypic selection, frequency of the B allele stabilized around 85% after 10 generations. For optimal selection, gene frequency increased linearly up to the last generation, at which point the optimal strategy moved the gene to fixation in the selected dams and to less than 20% in the selected sires. The optimal strategy thereby created a high frequency of heterozygotes (Bb) in the last generation, consistent with the objective of the strategy, which was to maximize the average genetic level in the final generation. Although this would not be a viable strategy to follow in practice, this example does illustrate that this procedure can in principle be used to optimize selection in dam and sire lines in a crossbreeding program, where the objective is to maximize performance of crossbred animals.
Discussion and conclusions
Results from this study clearly show that substantial benefits can be expected from use of a major gene in selection programs, provided the information on the major gene is incorporated properly in selection decisions. Injudicious selection on the major gene will result in less than maximal responses to selection in the short term , in particular for major genes with non-additive effects, and can even lead to reduced responses to selection in the longer term.
Results from this study show that selection on a major gene can be optimized and that optimal control theory is a suitable method to develop optimal selection strategies. Optimal control theory has been used extensively in engineering and economics to optimize multiple-stage decision problems with a structure similar to those described here. Optimal control theory allows development of computationally efficient algorithms to optimize such multiple-stage decision problems. For example, with a planning horizon of 10 generations, optimal values for the 40 decision variables involved (4 for each generation) were derived within 1 minute of CPU on an HP RISC workstation.
Optimal use of a major gene requires design of specific selection strategies toward a pre-specified selection objective. From a practical point of view, the choice of the selection objective is the most crucial decision to be made with regard to implementation of optimal strategies for use of a major gene. In this study, very simplified selection objectives were chosen, i.e. maximization of response after a fixed number of generations. Although such objectives serve to illustrate the principle of optimizing selection on a major gene, more complex objectives must be aimed for in practical breeding programs. An example would be maximization of cumulative discounted response to selection over a planning horizon of, e.g., 25 years. Such an objective combines short- and longer-term gains, with more emphasis given to short-term gains, depending on the discount factor used.
Optimal strategies derived in this study were based on a simplified deterministic model for genetic improvement. In this model, the effects of all other genes were modeled on the basis of the polygenic model of quantitative genetics and polygenic variance was assumed constant. Strictly, the derived strategies are optimal only under this model and the results may not hold up under more complex (and realistic) models. Although the strategies derived herein would ideally be tested in actual population, robustness of the optimal strategies to the specifics of the genetic model can be evaluated using stochastic computer simulation. Given the expense and time involved in selection experiments, computer simulation provides a viable alternative to test and validate alternative selection strategies.
To date, we have performed a limited degree of validation of our optimal strategies based on a stochastic simulation model. The main difference of this model with the deterministic model that was used for optimization is that polygenic variance is allowed to change as a result of selection. Preliminary results for selection on an additive major gene show that the extra benefits from the optimal strategies do hold up under stochastic simulation for longer planning horizons (5 and 10 generations) but not for a shorter planning horizon (3 generations). This is mainly due to the fact that the reduction in variance due to selection primarily occurs in the initial three generations, when the initial population is unselected. In practice, however, strategies for selection on a major gene will be implemented in already selected lines and the impact of the reduction of variance will be smaller.
The above does, however, indicate that there is scope for improving the deterministic model for which the optimal strategies are derived and, thereby, improving the applicability of results to practical breeding programs. This includes accounting for the effects of selection and inbreeding on genetic variance. In addition, selection on one major gene with known effects was considered here. Methods must be extended to simultaneous selection on multiple major genes, to selection on linked genetic markers, and to situations where the effect of the major gene is not known with certainty. In addition, the effects of alternate modes of gene action must be included, including epistatic interactions, gametic imprinting and polar overdominance.
Finally, we considered a simplified breeding program with single-stage selection in a closed population with discrete generations and for a trait for which phenotype was observed for all individuals prior to selection. Our study of this simplified scenario has provided a framework for optimization of more complex breeding programs and shown that there is substantial scope for improving the use of major genes in selection programs. Methods must, however, be extended to more complex and realistic breeding programs with multiple stage selection, overlapping generations, restrictions on availability of phenotypic records (e.g. sex-limited and carcass traits), as well as cross breeding programs. Methods must also be extended to the use of BLUP estimates of breeding values.
Acknowledgements
This research was initiated while the author was a visiting scientist at the Department of Animal Breeding in collaboration with Dr. Johan van Arendonk and on faculty at the Centre for Genetic Improvement of Livestock of the University of Guelph, Canada. Financial support from the Natural Sciences and Engineering Research Council of Canada, the Wageningen Agricultural Internation Exchange fund, the EU Human Capital and Mobility Research Network CHRX- CT94-0508, and the Iowa State University Agriculture and Home Economics Experiment Station is greatfully acknowledged
References
Dekkers, J.C.M. & van Arendonk, J.A.M. (1998) Optimizing selection for quantitative traits with information on an identified locus in outbred populations. Genetical Research 71: 257-275.
Dekkers, J. C. M., Birke, P. V. & Gibson, J. P. (1995). Optimum linear selection indexes for multiple generation objectives with non-linear profit functions. Animal Science 65, 165-175.
Falconer, D. S. &. Mackay, T. F. C (1996). Introduction to quantitative genetics. Harlow, UK: Longman.
Fournet, F., Elsen, J. M., Barbieri, M. E. & Manfredi, E. (1997) Effect of including major gene information in mass selection: a stochastic simulation in a small population. Genet. Sel. Evol. 29:35- 56.
Kuhn, M.T., Fernando, R.L. & Freeman, A.E. (1997) Response to mass versus quantitative trait locus selection under a finite loci model. J.Dairy Sci. 80(Suppl. 1):228 (Abstract)
Larzul, C., Manfredi, E. & Elsen, J. M. (1997) Potential gain from including major gene information in breeding value estimation. Genet. Sel. Evol.29:161- 184.
Lewis, F. L. (1986). Optimal control, New York: Wiley.
Meuwissen, T. H. E. & Goddard, M. E. (1996) The use of marker haplotypes in animal breeding schemes. Genet. Sel. Evol. 28:161-176.
Rothschild, M. F. (1998). Identification of quantitative trait loci and interesting candidate genes in the pig: progress and prospects. Proc. 6th World Congress on Genetics applied to Livestock Production. Vol. 26: 403-410.
Muir, W. M. & Stick, D. A. (1998). Relative advantage of combining genes with major effects in breeding programs: Simulation results. Proc. 6th World Congress on Genetics applied to Livestock Production. Vol. 26: 403-410.
Ruane, J. & Colleau, J. J. (1995). Marker assisted selection for genetic improvement of animal populations when a single QTL is marked. Genetical Research 66, 71-83.
Ruane, J. & Colleau, J. J. (1996). Marker-assisted selection for a sex-limited character in a nucleus breeding population. Journal of Dairy Science 79, 1666-1678.
Van der Beek, S. & van Arendonk, J. A. M. (1994). Marker assisted selection in a poultry breeding program. Proceedings of the 5th World Congress on Genetics Applied to Livestock Production, Guelph, 21, 237-240.
Woolliams, J. A. & Pong-Wong, R. (1995). Short- versus long-term responses in breeding schemes. Book of Abstracts, European Association of Animal Production, Prague.
[an error occurred while processing this directive]Questions and answers:
Dr. Allan Schinckel
- First comment for litter size, we currently have 100 sires and 150 sows in the Yorkshire breed with EPD's of plus one for number born alive. Thus in two years we could make 2.0 pigs born alive; however, the sires and dams would be related to each other and the population would be so inbred that there would be a loss of genetic improvement for all traits forever.
- If we would put all selection emphasis on litter size we could indeed make substantial progress for litter size without use of major genes or genetic markers, albeit at the risk of increasing inbreeding. Regardless of the impact on inbreeding, however, putting all emphasis on litter size would not allow us to make genetic progress for other economic traits. The fact remains, therefore, that for traits with low heritability, such as litter size, it is more difficult to make genetic progress using traditional means than for traits with higher heritability. Because progress from selection on major genes or genetic markers is to a much smaller degree determined by heritability, marker-assisted selection is in particular beneficial for low heritability traits.
- It seems that the model is a generalization that you have a major gene with dominance and everything else is totally additive and infinitely small. Won't you be better to model for example 5700 loci with a range of genetic effects including some dominance and epistasis?
- We indeed looked at a simplified model for polygenic effects, assuming they were determined by an infinite number of additive genes with small effect. Simulation studies by, e.g. Kuhn et al (1996) have, however, shown that so-called finite locus models, in which polygenes are similated by a limited number of individual genes, give similar comparisons between phenotypic and genotypic selection. We are planning to do similar simulation studies with finite locus models to determine the robustness of our optimal selection strategies to the genetic model used for polygenes.
Our assumption that dominance exists only for the major gene may not have a large impact on results. The reason for this is that, although non-additive effects likely exist for other genes, quantitative genetic selection approaches (can) only capitalize on their additive effects (apart from the use of crossbreeding). In fact, one of the advantages of selection on major genes or genetic markers is that it will enable us to capitalize on non- additive effects to a much greater degree.
Dr. Bill Muir
- What effect does genotypic selection have on the rate of inbreeding as compared to phenotypic selection?
- If a large amount of emphasis that is placed on the major gene, genotypic selection will tend to increase inbreeding compared to selection on own phenotype. This is because you will tend to select individuals with the same (favorable) genotype for the major gene, which will tend to be more related to each other. However, when this concept is extended to selection with use of BLUP EBV, major gene or marker-assisted selection will often reduce inbreeding, in particular for situations in which BLUP EBV rely heavily on pedigree or sib information (e.g. for low heritable traits or when own phenotype or progeny phenotype records are not available). In such cases, selection on BLUP EBV will tend to between-family selection because family members will have similar EBV due to the common pedigree or sib information. This increases inbreeding. Availability of information on a major gene or genetic marker will enable differentiation between family members that have received different alleles from their parents. This reduces the reliance on family information and decreases inbreeding. Note that, because DNA tests can be done at a very early age, information from major genes or genetic markers can be available prior to the age of selection.
* This paper was presented as part of the 1998 National Poultry Breeders Roundtable Discussions in St. Louis, MO. A more indepth discussion was made on Plant & Animal Genome VII held at St. Diego, CA (January 18-22, 1999).